Reinforcement learning – Apprendimento con rinforzo : prima parte

In questo articolo spiegherò i concetti alla base dell’apprendimento con rinforzo RL (Reinforcement Learning) e per consentire anche ai più curiosi un approfondimento spiegherò, successivamente, come implementare un piccolo software che consentirà di eseguire una simulazione sul comportamento di un “sistema” che tenta di perseguire un obiettivo spinto da una sollecitazione positiva. Prima di infilarci, però, come di consueto nei miei articoli, in tecnicismi dovuti, proverò ad affrontare in prima istanza l’argomento in modo semplificato.

Come ho già detto in altri articoli quando  si parla di apprendimento con rinforzo si fa riferimento a quei metodi di Machine Learning (ML) il cui training non viene effettuato preliminarmente, ma la macchina  apprende dai suoi errori.

La filosofia che c’è dietro alla tecnica dell’apprendimento con rinforzo è molto intuitiva e per spiegare il concetto mi limiterò a fare una similitudine con la vita reale ed in particolare con le tecniche di addestramento utilizzate per gli animali. Il processo di addestramento, infatti, è molto simile ed in generale si basa sul concetto di premio; Il metodo è il seguente: si da un reward positivo nel caso in cui “il soggetto” esegue un’azione corretta al più  un reward negativo o disincentivo nel caso contrario. Ovviamente si presume che il sistema abbia memoria, anche se su questo argomento approfondiremo in seguito nel dettaglio.

Per funzionare, pertanto, l’algoritmo di RL (Reinforcement Learning) prevede, sempre, per la sua implementazione, l’utilizzo di un agente ovvero di un soggetto/sistema, dotato di capacità di percezione, che esplora l’ambiente nel quale intraprende le azioni. Provando a dare una definizione più formale, possiamo dire che l’apprendimento per rinforzo (reinforcement learning) lavora partendo dall’osservazione dell’ambiente esterno, in cui ogni azione effettuata da un “agente” ne modifica lo stato, ed attraverso un meccanismo di retroazione (feedback) l’algoritmo tenderà a migliorarne l’apprendimento.

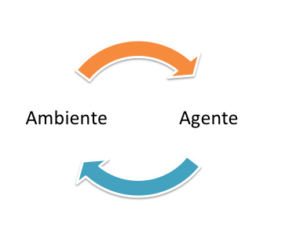
Proviamo a questo punto un approccio più pratico, per capirne la logica alla base, e per fare ciò approcceremo al problema attraverso un caso di studio semplice, costituito   da “un agente” in grado di compiere due sole azioni e supportato nel training con “dei premi” (reward) per raggiungere un unico obiettivo.

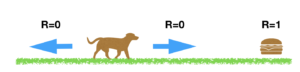
Il sistema che analizzeremo è costituito da “un agente” (un cane nel nostro esempio) in grado di muoversi su due direzioni destra e sinistra (Azioni) mentre il suo l’obiettivo sarà quello di raggiungere il cibo posizionato sul lato destro alla fine del percorso. Il sistema sarà libero di muoversi nelle due direzioni e riceverà sempre un reward = 0 (ovvero nessun premio R=0), in modo da non influenzare la scelta, mentre riceverà un premio positivo (supponiamo R=1) quando raggiungerà l’obiettivo.

Per facilitare il nostro studio, supporremo che l’agente possa muoversi facendo ogni volta un solo passo in una delle due direzioni e che per percorrere tutto il percorso dal punto di partenza siano sufficienti 5 passi.

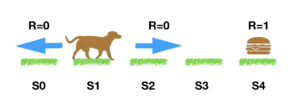
Il ragionamento è semplice: associamo ad ogni stato S (Step) un valore che identificherà la qualità dell’azione fatta nel passare da uno stato all’altro …. inizialmente può essere qualunque ma nel nostro caso ipotizzeremo che sia 0.

Se dovessimo quindi formalizzare il sistema Cane, potremmo considerare di utilizzare una matrice in cui inserire sulle colonne le azioni possibili e sulle righe gli stati (i passi) , quindi la situazione iniziale dei possibili stati  del cane (Agente) sarà semplicemente:

	Left	Right
0	0	0
1	0	0
2	0	0
3	0	0
4	0	0

Cerchiamo di capire come leggere la matrice.  Quando il cane si trova sullo step zero , sulla matrice si troverà ad esempio nello posizione (stato) indentificabile alle coordinate (0,Left) pertanto il cane potrà decidere di spostarsi a destra o restare dove di trova, dato che non esiste uno step -1, e lo farà in modo del tutto casuale in quanto il valore della matrice alle coordinate (0,Right) e (0,Left ) è uguale.

	Left	Right
0	0	0
1	0	0
2	0	0
3	0	0
4	0	0

Questo significa che è indiferrente l’azione che farà il cane, che inizialmente non sa cosa fare, in quanto, il valore della matrice è  inizializzata  a 0,   quindi esso è libero di  andare liberamente a destra o sinistra tanto ogni decisione è possibile ed è corretta.

Cosa farà dunque il cane nelle fasi inziali ?   l’agente ( cane) farà dei tentativi casuali fin quando non raggiungerà il premio, e poichè sarà in grado di “ricordare” in qualche modo  le azioni effettuate, cercherà di migliorare il suo comportamento tenendo in considerazione quanto fatto per via esperenziale.

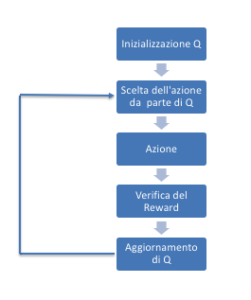
Abbiamo già capito, a questo punto, che la teoria si basa sulla necessità di aggiornare una matrice di valori,  che verrano modificati in fase di apprendimento con lo scopo di  amplificare le azioni corrette e di deamplificare quelle sbagliate. Il sistema filosofico alla base è semplice, ma l’implentazione dello stesso implica la conoscenza di alcuni concetti. La prima cosa che dobbiamo comprendere è il  modello matematico e di conseguenza l’algoritmo software in grado di tradurre lo stesso in codice utilizzabile. La letteratura,  in merito, tratta diverse soluzioni per risolvere questo problema noi ci soffermeremo su uno in particolare detto  Q-Learning.

In questa fase proviamo a lavorare partento da un presupposto, ovvero accettiamo per assodato che i valori della matrice Q si aggiornano secondo la seguente formula ricorsiva:

che viene implementata attraverso il seguente algorittimo:

while not is_terminated:

A = self.choose_action(S, q_table)
S_, R = self.get_env_feedback(S, A) # take action & get next state and reward
q_predict = q_table.loc[S, A]
if S_ != 'terminal':
q_target = R + GAMMA * q_table.iloc[S_, :].max() # next state is not terminal
else:
q_target = R # next state is terminal
is_terminated = True # terminate this episode

q_table.loc[S, A] += ALPHA * (q_target - q_predict) # update

S = S_ # move to next state

Proviamo ad approfondire il concetto descritto precedentemente introducendo i necessari formalismi e per fare ciò, riprendiamo le ipotesi di base di uno scenario di Reinforcement Learning: Ipotizziamo che in un tipico scenario di apprendimento  :  Un agente eseguirà  delle azioni che indentificheremo con la lettera (a); sappiamo che  tali azioni modificheranno l’ambiente spigendo il sistema ad un cambiamento di stato  che indicheremo con la lettera (s).  Durante le prove l’agente riceverà una ricompensa o reward che in futuro sarà indicato con la lettera (r). Definiremo inoltre episodio una sequenza finita di stati, azioni, reward.

In ciascun stato , l’obiettivo è quello di scegliere l’azione ottimale , ovvero quella che massimizza il future Reward  definito in generale come:

in molte applicazioni, però, si utilizza il Discount Future Reward definito come:

 con 

Il discount future reward può essere dunque definito ricorsivamente come:

in definitiva la funzione Q(s,a) già introdotta precedentemente indica la qualità o l’ottimalità dell’azione a quando ci si trova in uno stato s.

Ma di questo ne parleremo nel prossimo articolo. Per il momento potete testare l’algorittimo utilizzando un piccolo software di cui vi lascio il codice di esempio  qui

seconda parte >>