
Che cosa è la matrice di correlazione? come si costruisce in Python?
AI, INTELLIGENZA ARTIFICIALE, MATEMATICA, Senza categoria, TUTORIAL
Che cosa è la matrice di correlazione? Per rispondere a questa domanda iniziamo con imparare una definizione:
La matrice di correlazione è una tabella quadrata che riporta al suo interno gli indici di correlazione tra due o più variabili.

Prima di addentrarci nel capire come costruire una matrice di correlazione e come leggerla cerchiamo di ricordare il concetto di Correlazione e di comprenderne il significato.
Cos’è la correlazione?
La correlazione è una misura statistica che esprime la relazione tra due variabili ed indica la tendenza che hanno due variabili (X e Y) a variare insieme, ovvero, a “covariare”. Ad esempio, si può supporre che vi sia una relazione tra peso ed altezza di un individuo , nel senso che all’aumentare dell’altezza ad esempio aumenta il peso.
Le correlazioni possono essere ti tipo Lineare e non Lineare.
Correlazione Lineare
La relazione è di tipo lineare se l’andamento tra le due variabili osservate, assume su un sistema di assi cartesiani la forma di una retta. In questo caso, all’aumentare (o al diminuire) di X aumenta (diminuisce) Y. Ad esempio, all’aumentare dell’altezza di una persona aumenta anche il suo peso
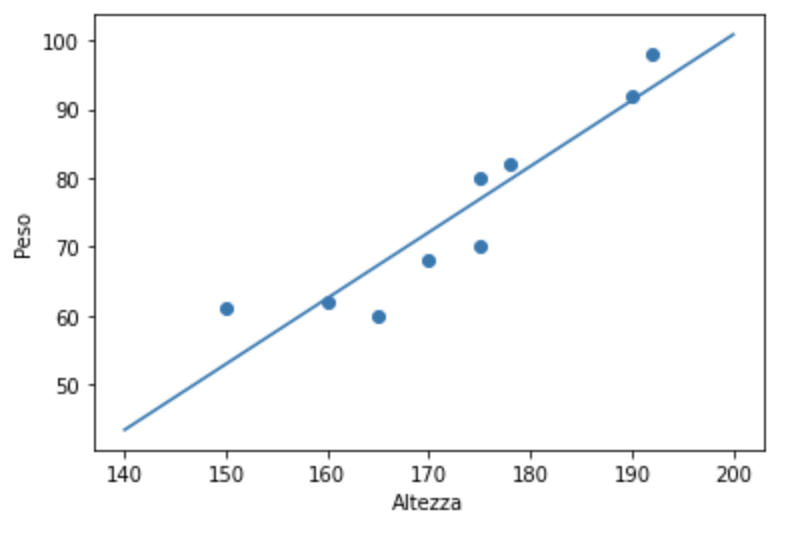
Correlazione non lineare
La relazione è di tipo non lineare, se rappresentata su assi cartesiani, ha un andamento curvilineo (parabola o iperbole). In questo caso a livelli bassi e alti di X corrispondono livelli bassi di Y; mentre a livelli intermedi di X corrispondono livelli alti di Y.
Forma della correlazione
Per quanto riguarda la forma della relazione, si distinguono l’entità e la direzione.
La direzione è positiva, se all’aumentare di una variabile aumenta anche l’altra. Ad esempio, all’aumentare della superficie aumenta aumento il prezzo dell’immobile.
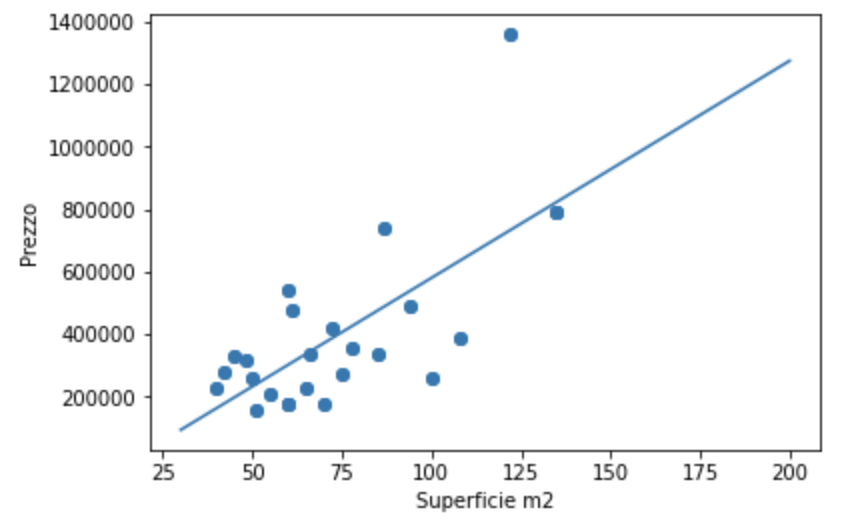
La direzione è , invece, negativa se all’aumentare di una variabile diminuisce l’atra, ad esempio all’aumentare della produzione di un prodotto in genere il prezzo del prodotto diminuisce. In pratica all’aumentare dell’offerta il prezzo precipita.
Un altro modo per differenziare le correlazioni è osservando l’entità, ovvero alla forza della relazione esistente tra due variabili. L’entità spiega quanto sia forte la correlazione osservando i punti nello spazio di dispersione, in pratica quanto più i punteggi sono raggruppati attorno ad una retta, tanto più forte è la relazione tra due variabili.
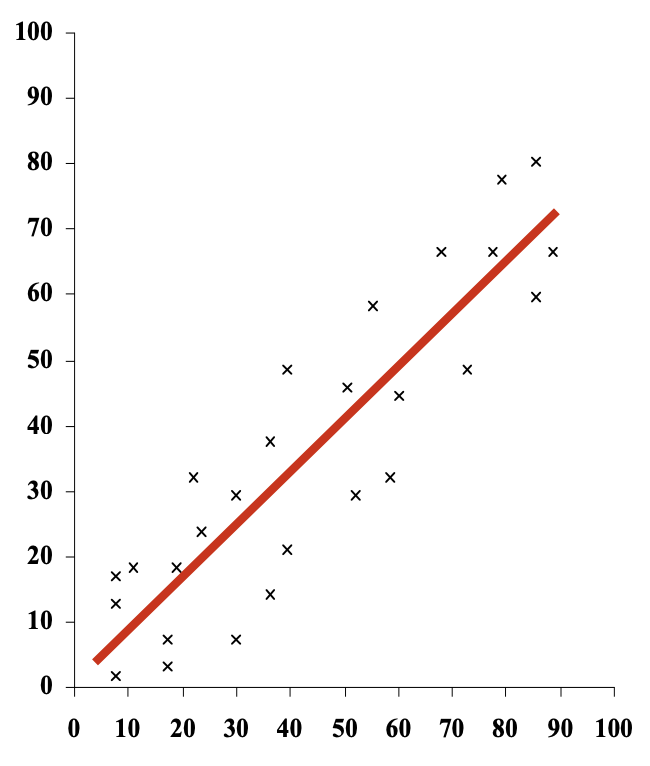
Se i punteggi sono dispersi in maniera uniforme, invece, tra le due variabili non esiste alcuna relazione.
Come si misura?
Per esprimere la relazione esistente tra due variabili, in termini entità e direzione, si utilizza il coefficiente di correlazione. Tale coefficiente è standardizzato e può assumere valori che vanno da –1.00 (correlazione perfetta negativa) e +1.00 (correlazione perfetta positiva). Una correlazione uguale a 0 indica che tra le due variabili non vi è alcuna relazione
Quali limitazioni ha l’analisi della correlazione?
La correlazione non è in grado di verificare la presenza o l’effetto di altre variabili che non siano le due prese in esame. In particolare, non ci dice niente di causa ed effetto
Coefficienti di correlazione
La correlazione viene descritta mediante un valore che non è dotato di un’unità di misura specifica, chiamato coefficiente di correlazione, compreso tra -1 e +1 e denotato da r.
In riferimento all’indice di correlazione r possiamo affermare che:
- Più r si avvicina a zero, più la correlazione lineare è debole.
- Un valore r positivo è indice di una correlazione positiva, in cui i valori delle due variabili tendono ad aumentare in parallelo.
- Un valore r negativo è indice di una correlazione negativa, in cui il valore di una variabile tende ad aumentare quando l’altra diminuisce.
sono stai formulati di versi coefficienti di correlazione a seconda del tipo di scala della variabile, in particolare dobbiamo ricordare:
- Per le scale a intervalli o rapporti equivalenti si usa il coefficiente r di Pearson.
- Per le scale ordinali si usano il coefficiente rs di Spearman o il coefficiente tau di Kendall.
- Per le scale categoriali (dicotomiche) si usano il coefficiente rphi o il coefficiente rpbi
Come si può creare la matrice di correlazione in Python?
Per prima cosa dobbiamo procurarci un dataset per poter effettuare le nostre elaborazioni ed allo scopo ho deciso di costruire un dataset, relativo alla distribuzione dei prezzi degli immobili in funzione di alcune variabili:
1) prezzo
2) numero di locali
3) superficie in metri quadri
4) numero di bagni
Per fare ciò vi sottopongo un script per raccogliere velocemente dei dati da internet a solo scopo didattico.
import requests
from bs4 import BeautifulSoup
from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd
a_prezzo=[]
a_locali=[]
a_m2superficie=[]
a_bagni=[]
a_piano=[]
NUMERO_DI_PAGINE=20
for index in range(0,NUMERO_DI_PAGINE,1):
print (index)
page = 'https://www.immobiliare.it/vendita-case/milano/?pag='+str(index)
web_result = requests.get(page).text
soup = BeautifulSoup(web_result,'lxml')
for ul in soup.findAll('ul',{'class':'in-realEstateListCard__features'}):
li=ul.findAll('li',{'class':'nd-list__item'});
try:
prezzo=str(li[0].text)
except Exception as e:
prezzo="ND"
try:
locali=str(li[1].text).strip()
except Exception as e:
locali="ND"
try:
m2superficie=str(li[2].text).strip()
except Exception as e:
m2superficie="ND"
try:
bagni=str(li[3].text).strip()
except Exception as e:
bagni="ND"
try:
piano=(li[4].text).strip()
except Exception as e:
piano="ND"
try:
p = float(prezzo.replace('€ ','').replace('.',''))
except Exception as e:
p = 0
try:
l = int(locali)
except Exception as e:
l = 0
try:
b = int(bagni)
except Exception as e:
b = 0
try:
s = int(m2superficie.replace('m²',''))
except Exception as e:
s = 0
if (p > 0) and (l > 0) and (b > 0) and (s > 0):
a_prezzo.append(p)
a_locali.append(l)
a_m2superficie.append(s)
a_bagni.append(b)
df = pd.DataFrame({'prezzo': a_prezzo, 'locali': a_locali, 'm2superficie': a_m2superficie,'bagni' : a_bagni})
df.to_csv('./dataset.csv')
Questo script vi restituirà un dataset in formato csv.. dovreste ottenere qualcosa del genere
| prezzo | locali | m2superficie | bagni | |
|---|---|---|---|---|
| 0 | 279000.0 | 3 | 70 | 1 |
| 1 | 170000.0 | 2 | 47 | 1 |
| 2 | 790000.0 | 3 | 135 | 2 |
| 3 | 385000.0 | 2 | 65 | 1 |
| 4 | 290000.0 | 3 | 70 | 1 |
| … | … | … | … | |
| 419 | 295000.0 | 3 | 90 | 1 |
| 420 | 1290000.0 | 4 | 145 | 3 |
| 421 | 1560000.0 | 5 | 195 | 3 |
| 422 | 280000.0 | 2 | 55 | 1 |
| 423 | 130000.0 | 2 | 40 |
Adesso cerchiamo di capire come possiamo generare un array di correlazione usando il metodo DataFrame.corr() e visualizzare la matrice di correlazione usando il metodo pyplot.matshow() in Matplotlib. Useremo il DataFrame ottenuto per generare e visualizzare un array di correlazione.
Generazione della matrice di correlazione utilizzando il metodo DataFrame.corr()
Carichiamo dal dataset solo le colonne di nostro interesse: [‘prezzo’, ‘locali’,’m2superficie’,’bagni’] e costruiamo al matrice di correlazione
import pandas as pd
fields = ['prezzo', 'locali','m2superficie','bagni']
immobili_df = pd.read_csv ('dataset.csv', skipinitialspace=True, usecols=fields)
print(immobili_df.head())
corr_df = immobili_df.corr()
print("The correlation DataFrame is:")
print(corr_df, "\n")
il risultato sarà qualcosa del genere:

Il metodo utilizzato genera un DataFrame con valori di correlazione tra ogni colonna con ogni altra colonna nel DataFrame.
I valori di correlazione sono calcolati di default usando l’indice di correlazione di Pearson. Possiamo anche usare altri metodi come kendall e spearman per calcolare il coefficiente di correlazione specificando il valore del parametro method nel metodo corr.
ad esempio per utilizzare il coefficiente di correlazione kendall :
corr_df = immobili_df.corr(method='kendall')
corr_df = immobili_df.corr(method='pearson')
corr_df = immobili_df.corr(method='spearman')
Matrice di correlazione di Pandas usando il metodo seaborn.heatmap()
Con questo approccio possiamo graficare la matrice di correlazione generata dal DataFrame immobili_df utilizzando la funzione heatmap() del pacchetto seaborn.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
fields = ['prezzo', 'locali','m2superficie','bagni']
immobili_df = pd.read_csv ('dataset.csv',skipinitialspace=True,usecols=fields)
corr_df = immobili_df.corr(method='pearson')
plt.figure(figsize=(8, 6))
sns.heatmap(corr_df, annot=True)
plt.show()
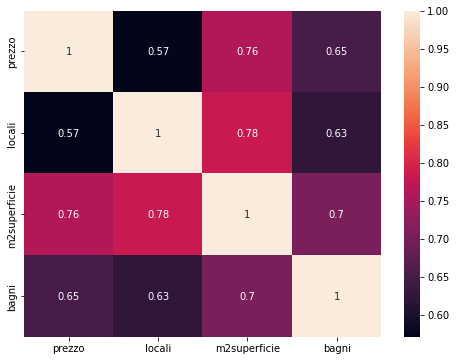
Matrice di correlazione utilizzando DataFrame.style
La proprietà style dell’oggetto DataFrame corr_df restituisce un oggetto Styler. In tal caso sarà possibile visualizzare l’oggetto DataFrame usando background_gradient per l’oggetto Styler. Attenzione : Questo metodo può generare solo figure nel notebook IPython.
import pandas as pd
fields = ['prezzo', 'locali','m2superficie','bagni']
immobili_df = pd.read_csv ('dataset.csv',skipinitialspace=True,usecols=fields)
corr_df = immobili_df.corr(method='pearson')
corr_df.style.background_gradient(cmap='coolwarm')


Sono amante della tecnologia e delle tante sfumature del mondo IT, ho partecipato, sin dai primi anni di università ad importanti progetti in ambito Internet proseguendo, negli anni, allo startup, sviluppo e direzione di diverse aziende; Nei primi anni di carriera ho lavorato come consulente nel mondo dell’IT italiano, partecipando attivamente a progetti nazionali ed internazionali per realtà quali Ericsson, Telecom, Tin.it, Accenture, Tiscali, CNR. Dal 2010 mi occupo di startup mediante una delle mie società techintouch S.r.l che grazie alla collaborazione con la Digital Magics SpA, di cui sono Partner la Campania, mi occupo di supportare ed accelerare aziende del territorio .
Attualmente ricopro le cariche di :
– CTO MareGroup
– CTO Innoida
– Co-CEO in Techintouch s.r.l.
– Board member in StepFund GP SA
Manager ed imprenditore dal 2000 sono stato,
CEO e founder di Eclettica S.r.l. , Società specializzata in sviluppo software e System Integration
Partner per la Campania di Digital Magics S.p.A.
CTO e co-founder di Nexsoft S.p.A, società specializzata nella Consulenza di Servizi in ambito Informatico e sviluppo di soluzioni di System Integration, CTO della ITsys S.r.l. Società specializzata nella gestione di sistemi IT per la quale ho partecipato attivamente alla fase di startup.
Sognatore da sempre, curioso di novità ed alla ricerca di “nuovi mondi da esplorare“.


Comments